An Introduction to Chaos and Fractals
Chaos theory is a fascinating field at the frontier of science, mathematics, and art. It reveals a hidden order in systems that appear random but are, in fact, deterministic. From the intricate patterns in nature to complex engineering problems, chaos provides a new lens through which to understand the world. This page offers a simple, illustrated tour of its core concepts.
The Logistic Map: A Simple Path to Chaos
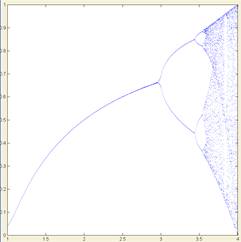
Chaotic behavior is often found in simple iterated systems. A classic example is the Logistic Map, a model used to simulate population dynamics. As you vary a single parameter ('c'), the system's long-term behavior transitions from a stable equilibrium to predictable oscillations, and finally into a state of chaos where the population never repeats.
This journey reveals a universal pattern known as period-doubling, governed by the Feigenbaum constant, proving that even within chaos, there is profound underlying order.
2D & 3D Strange Attractors
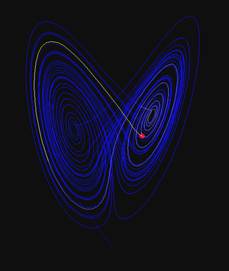
Expanding into more dimensions, we find Strange Attractors. These are sets of points towards which a system evolves over time. For certain parameters, the path of the system forms an intricate, never-repeating fractal curve.
Whether it's a 2D system like the Quadratic Map or a 3D system like the famous Lorenz Attractor (derived from atmospheric models), these attractors visualize the complex, bounded, and yet unpredictable nature of chaos.
Basins of Attraction in the Complex Plane
Chaos also appears beautifully in the complex plane. When using an algorithm like the Newton-Raphson method to find the roots of a complex equation (e.g., finding `z` where `z³ - 1 = 0`), the complex plane can be colored based on which root each starting point converges to.
The regions of color are called Basins of Attraction. The boundaries between these basins are not simple lines but infinitely complex fractals, revealing a hidden world of intricate detail.
Mandelbrot & Julia Sets: The Stars of the Fractal World
Perhaps the most famous fractal is the Mandelbrot Set. It is a "catalog" of all possible Julia sets. Each point `c` on the complex plane corresponds to a unique Julia set, and the Mandelbrot set itself is the collection of all points `c` for which the corresponding Julia set is connected.
The boundary of the Mandelbrot set is infinitely complex. No matter how much you zoom in, new and intricate details emerge, including miniature copies of the set itself—a property known as self-similarity.
Generating Nature: L-Systems and Procedural Fractals
The principles of fractal geometry and iterative systems are remarkably effective at modeling natural forms. Lindenmayer Systems (L-Systems) are a set of rules and symbols that can generate complex structures, like plants and trees, from a simple starting string. This mimics the biological process of growth.
Other techniques, like the "folded plane" method, use random fractal noise to generate realistic-looking clouds and landscapes. These methods are a cornerstone of modern computer graphics for creating natural-looking environments.